5092. Соты
Пчела, находясь в пчелиных сотах, может передвигаться так,
как показано на рисунке:
·
ходами 1 и 2 – из верхнего ряда,
·
ходом 3 – из нижнего ряда.
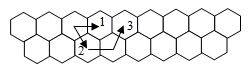
Вход. Количество шестиугольников n (1 ≤ n ≤
45) в верхнем ряду. В нижнем ряду шестиугольников на 1 меньше.
Выход. Выведите количество
способов, которыми пчела может добраться из первой клетки верхнего ряда в
последнюю клетку этого же ряда.
|
Пример
входа |
Пример
выхода |
|
3 |
2 |
РЕШЕНИЕ
числа
Фибоначчи
Анализ алгоритма
Пронумеруем все соты
последовательно слева направо, сверху вниз, как показано на рисунке. При этом:
·
соты верхнего ряда имеют нечётные номера;
·
соты нижнего ряда имеют чётные номера.
Если в верхнем
ряду содержится n сот, то самая правая сота верхнего ряда будет иметь номер 2n
– 1.
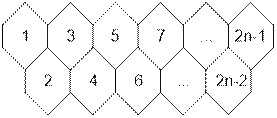
Обозначим через f(k) количество способов попасть из первой
соты в соту с номером k. Поскольку пчела должна попасть в соту номер 2n – 1, то ответом к задаче будет значение f(2n – 1).
Рассмотрим
переходы по сотам.
· Пусть сота k находится в
верхнем ряду (нечётный номер). Тогда пчела может попасть в неё либо из соты с номером k – 2, либо из соты с номером k – 3. Следовательно, для
нечётных k выполняется рекуррентное соотношение:
f(k) = f(k
– 2) + f(k – 3)
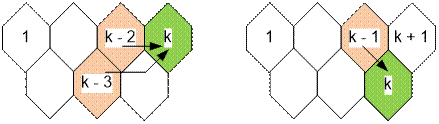
·
Пусть сота k находится в нижнем ряду (чётный номер). Тогда возможен только один вариант
перехода – из предыдущей соты:
f(k) = f(k
– 1)
Для реализации
рекурсии необходимо
задать начальные значения:
f(1) = 1, f(2) =
1, f(3) = 1
Они легко проверяются
напрямую по схеме движения пчелы.
Реализация алгоритма
Объявим рабочий
массив.
#define MAX 100
int fib[MAX];
Заполним элементы массива fib в соответствии с рекуррентным
соотношением.
fib[0] = 0;
fib[1] = 1; fib[2] = 1;
for (int
i = 3; i < MAX; i++)
if (i % 2 ==
1) fib[i] = fib[i-2] + fib[i-3];
else fib[i] =
fib[i-1];
Читаем значение n и
выводим ответ f(2n – 1).
scanf("%d",&n);
printf("%d\n",fib[2*n-1]);
Реализация алгоритма –
рекурсия + запоминание
Объявим рабочий
массив.
int fib[90];
Реализуем рекурсивное вычисление функции f с использованием
мемоизации.
int f(int
n)
{
if (n == 1) return 1;
if (n == 2) return 1;
if (n == 3) return 1;
if (fib[n] !=
-1) return fib[n];
if (n % 2 ==
1) return fib[n] = f(n - 1) + f(n - 3);
return fib[n]
= f(n - 1);
}
Основная часть программы. Читаем входное значение n.
scanf("%d",&n);
Вычисляем и выводим ответ.
memset(fib,-1,sizeof(fib));
printf("%d\n",f(2*n-1));
Java реализация
import java.util.*;
public class Main
{
static int fib[] = new int[90];
static int f(int n)
{
if (n <= 3) return 1;
if (fib[n] != -1) return fib[n];
if (n % 2 == 1) return fib[n] = f(n - 1) + f(n
- 3);
return fib[n] = f(n - 1);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
Arrays.fill(fib, -1);
System.out.println(f(2*n-1));
con.close();
}
}